Semialgebraic space

In mathematics, especially in real algebraic geometry, a semialgebraic space is a space which is locally isomorphic to a semialgebraic set.

Definition

Let U be an open subset of Rn for some n. A semialgebraic function on U is defined to be a continuous real-valued function on U whose restriction to any semialgebraic set contained in U has a graph which is a semialgebraic subset of the product space Rn×R. This endows Rn with a sheaf 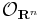\mathcal{O}_{\mathbf{R}^n} of semialgebraic functions.

(For example, any polynomial mapping between semialgebraic sets is a semialgebraic function, as is the maximum of two semialgebraic functions.)

A semialgebraic space is a locally ringed space 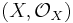(X, \mathcal{O}_X) which is locally isomorphic to Rn with its sheaf of semialgebraic functions.

See also